Among many models which explain the Coulomb-Amontons law of friction, an interesting model is based on the damage rheology. Dr. Vladimir Lyakhovsky, whom I visited recently at the Geological Survey of Israel in Jerusalem, has explained to me the details of this model. It is based on the idea of a phase transition between an elastic solid and granular media. Below is a phase transition diagram from the paper V. Lyakhovsky & Y. Ben-Zion, 2014, Damage–breakage rheology model and solid-granular transition near brittle instability, J. Mech. Phys. Solids 64:184–197.

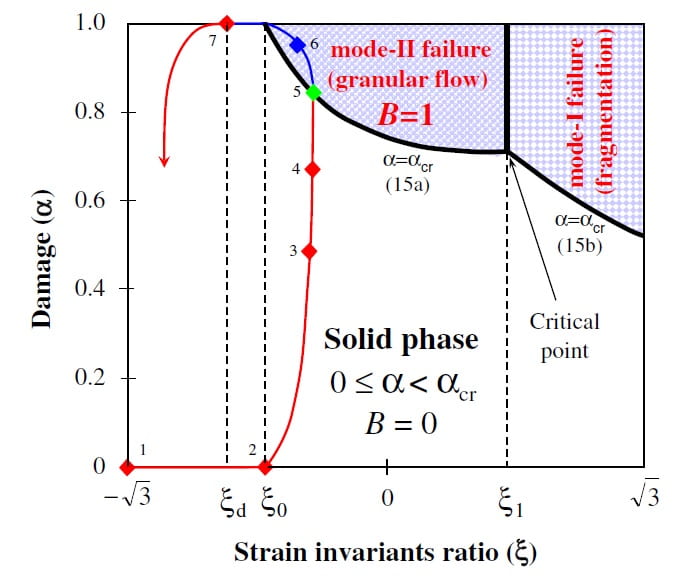
You can see three phases (solid, liquid, and even gas). Pseudo-“liquid” flow is of course somewhat similar to the plasticity, whereas “gas” is just the fragmentation of granular particles.

However, one can ask a question, whether the “solid-liquid” (= elastic-plastic) phase transition is that of the first or of the second order? We tend to think about these transitions as the second order transitions, as opposed to the “true” transitions between the aggregate states of the material. However, somewhat surprisingly (at least for those who did not know that), there is a latent heat associated with the onset of the plastic flow. It is similar to ice melting (i.e., the first order phase transition)! There is a classical work about that:
G. I. Taylor & H. Quinney, 1934, The Latent Energy Remaining in a Metal after Cold Working, Phil. Trans. R. Soc. A 143:307 (DOI: 10.1098/rspa.1934.0004).