Our review paper about the Voronoi entropy.
Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.E.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy 2018, 20, 956.
https://www.mdpi.com/1099-4300/20/12/956
The Voronoi entropy is a mathematical tool for quantitative characterization of the orderliness of points distributed on a surface. The tool is useful to study various surface self-assembly processes. We provide the historical background, from Kepler and Descartes to our days, and discuss topological properties of the Voronoi tessellation, upon which the entropy concept is based, and its scaling properties, known as the Lewis and Aboav–Weaire laws. The Voronoi entropy has been successfully applied to recently discovered self-assembled structures, such as patterned microporous polymer surfaces obtained by the breath figure method and levitating ordered water microdroplet clusters.
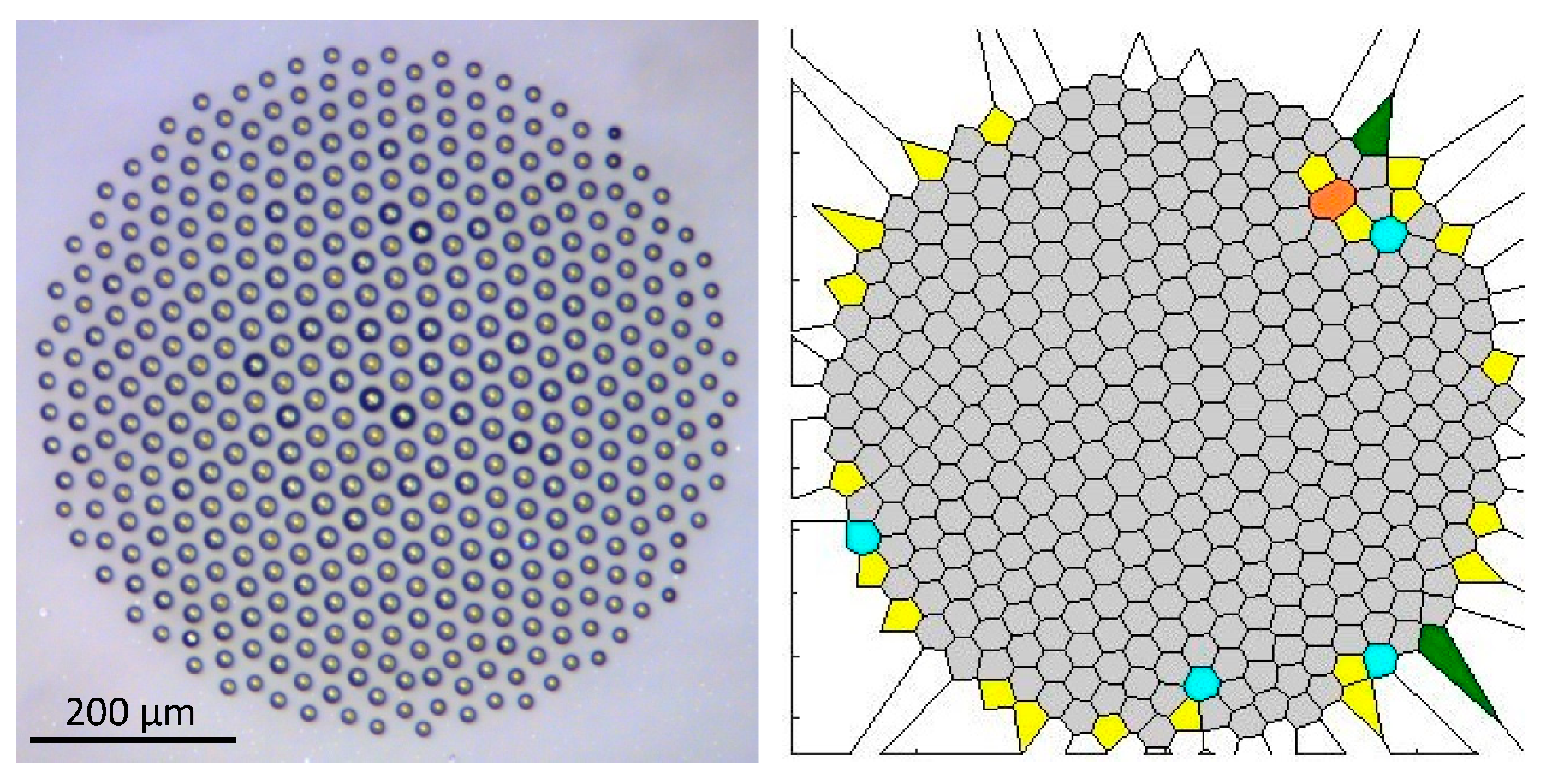
A a relatively large droplet cluster and its Voronoi diagram. The structure of the cluster is ordered at the center, while there are defects at the periphery. The value of the Voronoi entropy is Svor = 0.335