The Kapitsa pendulum (an inverted pendulum on a vibrating foundation), which is stabilized due to fast high frequency vibrations of a foundation, is an example of how vibrations can be substituted by an effective force. A mathematical technique of averaging the fast vibration is called the method of separation of motions. It is amazing how many interesting and counter-intuitive non-linear effects small vibrations can cause: changing the bending stiffness of elastic beams, turning granular material into effective liquid, jamming or opening pipes and pores for water flow, synchronizing motion, propulsion in fluids, and many others. Russian mechanician Prof. Ilya Blekhman even suggested a new area of “Vibrational mechanics” to deal with these diverse effects.

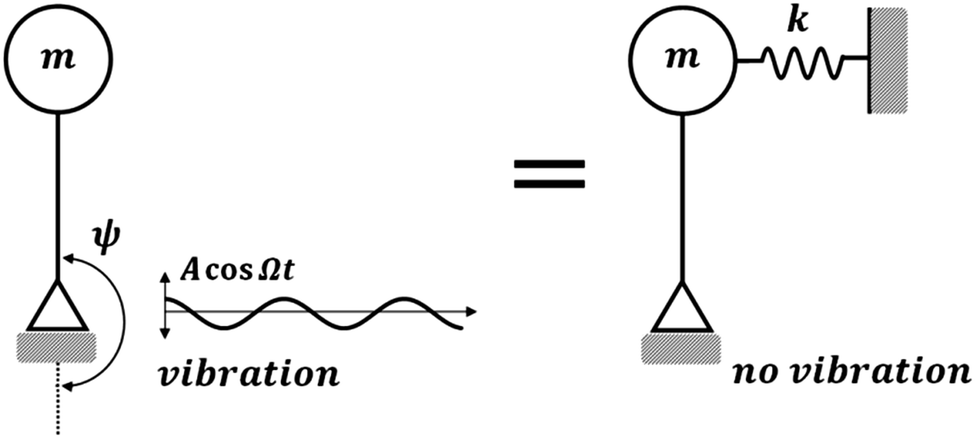
An inverted pendulum on a foundation vibrating with a periodic displacement Acos(Ωt) can be represented as an inverted pendulum stabilized by a spring k.

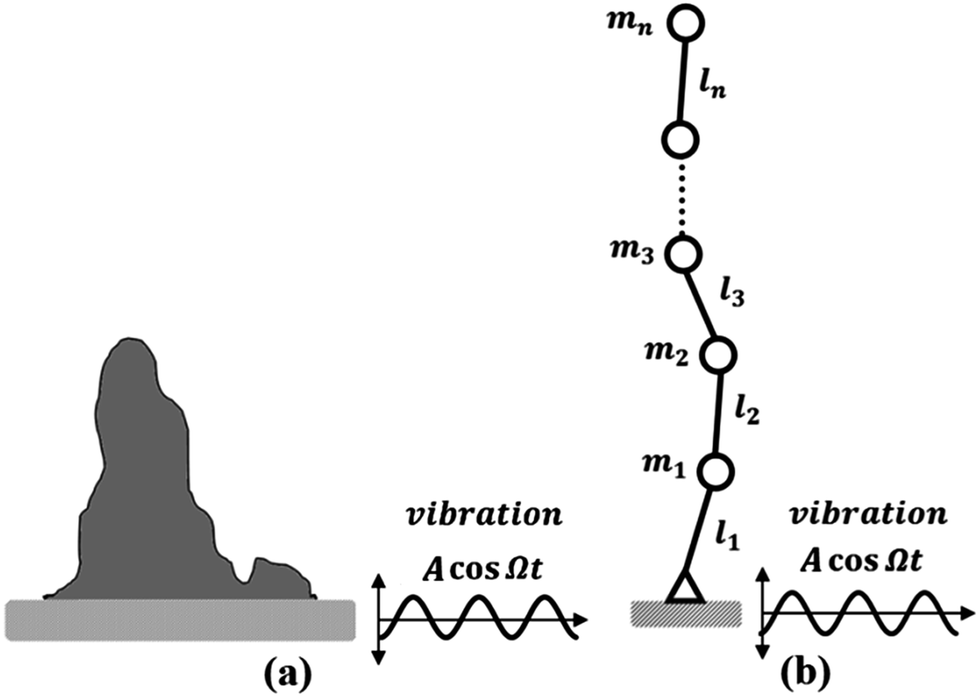
An analogy between (a) rising of a non-Newtonian liquid (“Cornstarch monsters”) on a vibrating foundation and (b) multiple pendulums on a vibrating foundation. (R. Ramachandran & M. Nosonovsky, 2014, “Vibro-levitation and inverted pendulum: parametric resonance in vibrating droplets and soft materials” Soft Matter, 10:4633)

Together with my student Dr. Rahul Ramachandran, we applied the same concept to the phase transition and various effects related to liquid droplets. There are many situations in which small fast vibrations can be substituted by effective forces or potentials, and they affect the stability or a phase state of a physical system.

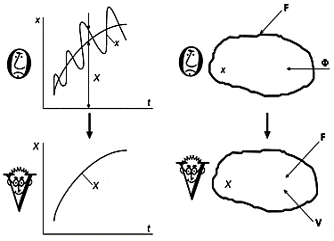
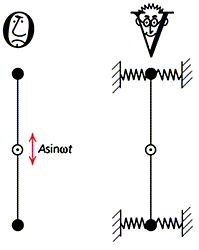
Blekhman’s interpretation of the effect of small-amplitude fast vibrations: Two “observers”, “O” can see small vibrations, “V” observes an effective force instead. The effective vibrational force is somewhat similar to the inertia force (it is not a real force). For the pendulum on a vibrating foundation, “V” sees an effective spring force. (Blekhman I.I. Vibrational Mechanics – a General Approach to Solving Nonlinear Problems. In: Ed. Elishakoff I, Mechanical Vibration: Where do we stand? Springer, New York 2007)

Recently I visited a lab of my colleague and friend Dr. Abba Priev at Hadassah Medical School of the Hebrew University in Jerusalem. They use very fast ultrasound vibrations for various purposes from investigating properties of liquids (ultrasound spectroscopy) to separation of phases in a multi-phase flow and extraction of micro/nanoparticles, cells, and bacteria from various liquids including milk, wine, water-oil mixtures, blood, and even semen (to separate healthy and unhealthy sperm cells for in-vitro fertilization procedures).

Wave beam in a cylindrical resonator for separation of cells in milk. The concentration of fat and protein in milk inside an acoustic resonator (L. Ostrovsky 2015 “Concentration of microparticles and bubbles in standing waves” J. Acoustical Soc. Am. 138:3607; L. Ostrovsky, A. Priev et al. 2012 “Acoustic radiation force for rapid detection of particles in biological liquids,” Proc. Meet. Acoust. 14:020002)

The situation is very similar to the “vibrational mechanics”. There are fast small amplitude vibrations (the ultrasound). The result is an effective force, which drives the particles into the nodes of the vibration mode shapes. There are many interesting mechanical problems involving these effect (for example, why cylindrical resonators work better than rectangular ones).

UPDATE. See also: Vibrational separation of fractions for anti-microbial brass