Surface tension is a fundamental concept in surface physics and chemistry. The most common definition of surface tension is that it is a force acting along a line of unit length parallel to the surface, but perpendicular to the line. However, mechanical forces are vectors, and they are applied to bodies or material points (particles). Unlike conventional mechanical forces, the surface tension forces are not applied to the three-phase line, which is a geometrical line and not a material object with a mass.

In our relatively recent paper we revisited the concept of the surface tension and argued that the surface tension is a generalized force (a derivatives of the interfacial energies by the distance for which the three-phase line advances), rather than a conventional mechanical force. These forces reflect the tendency of the system to reduce its energy (and increase entropy). We suggested a simple geometric interpretation of the Young, Wenzel, Cassie, Antonoff and Girifalco–Good equations for the equilibrium during wetting as well as of contact angle hysteresis.

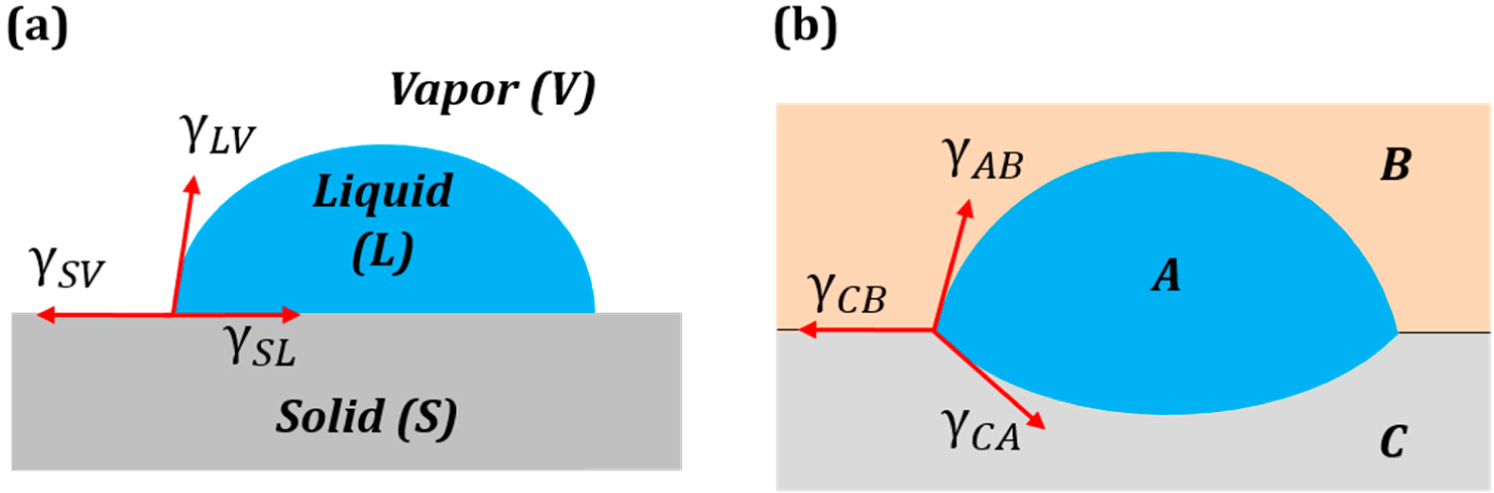
Figure 1. (a) Surface tension forces at the three-phase line on a non-deformable solid surface. The vertical components of the forces remain unbalanced and acts upon the solid substrate causing its deformation. (b) An ideal description of the equilibrium, the solid substrate (S) is deformed and the forces are balanced.

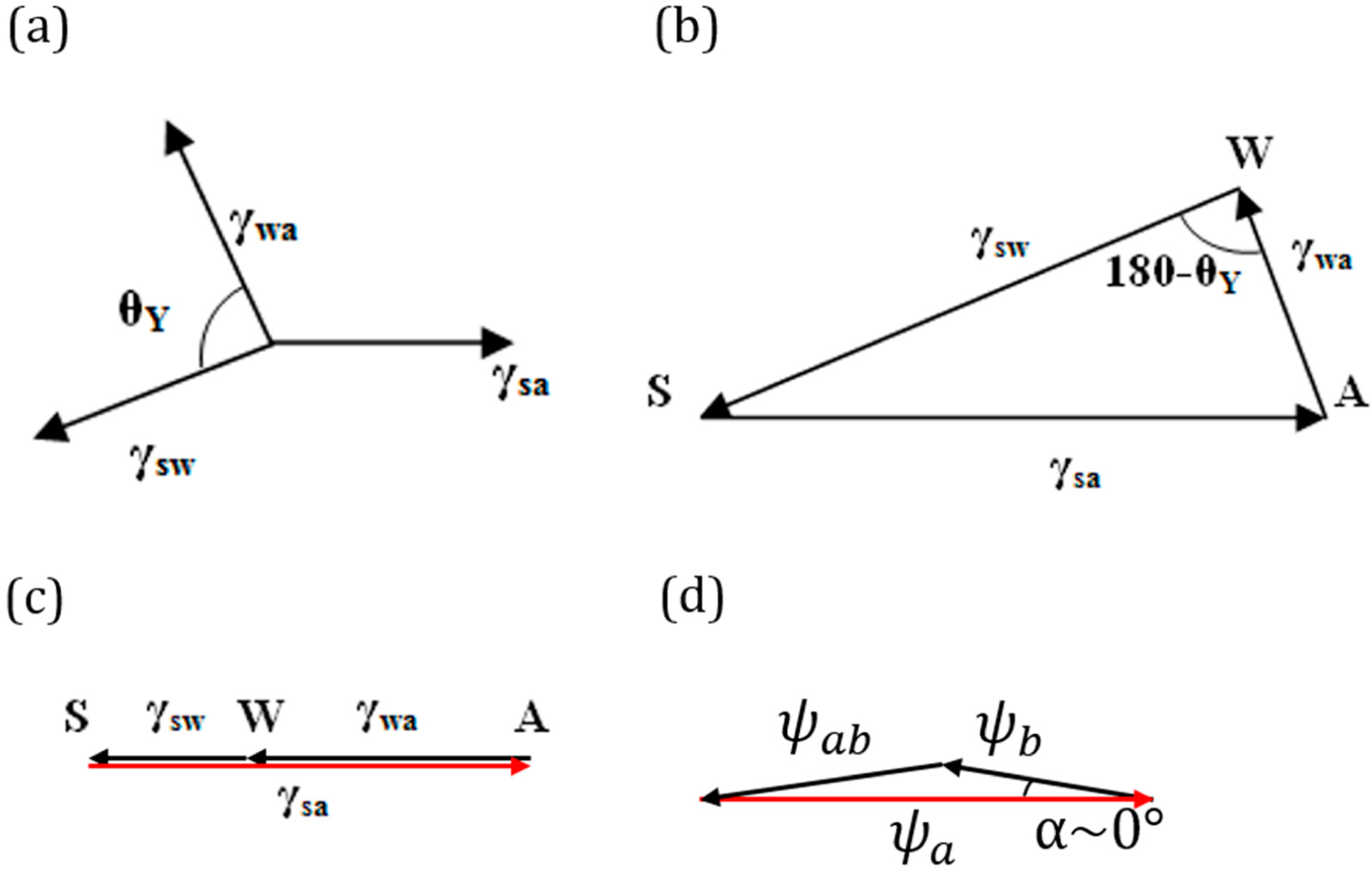
Figure 2. Various geometric interpretations of the vector equilibrium. (a) Equilibrium of surface tension vectors at the three-phase line; (b) Neumann’s triangle for a three-phase system; (c) when Antonoff’s rule is an exact equality, the surface tension vectors lie on the same line; this corresponds to complete wetting; (d) geometric interpretation of the Girifalco and Good equation.

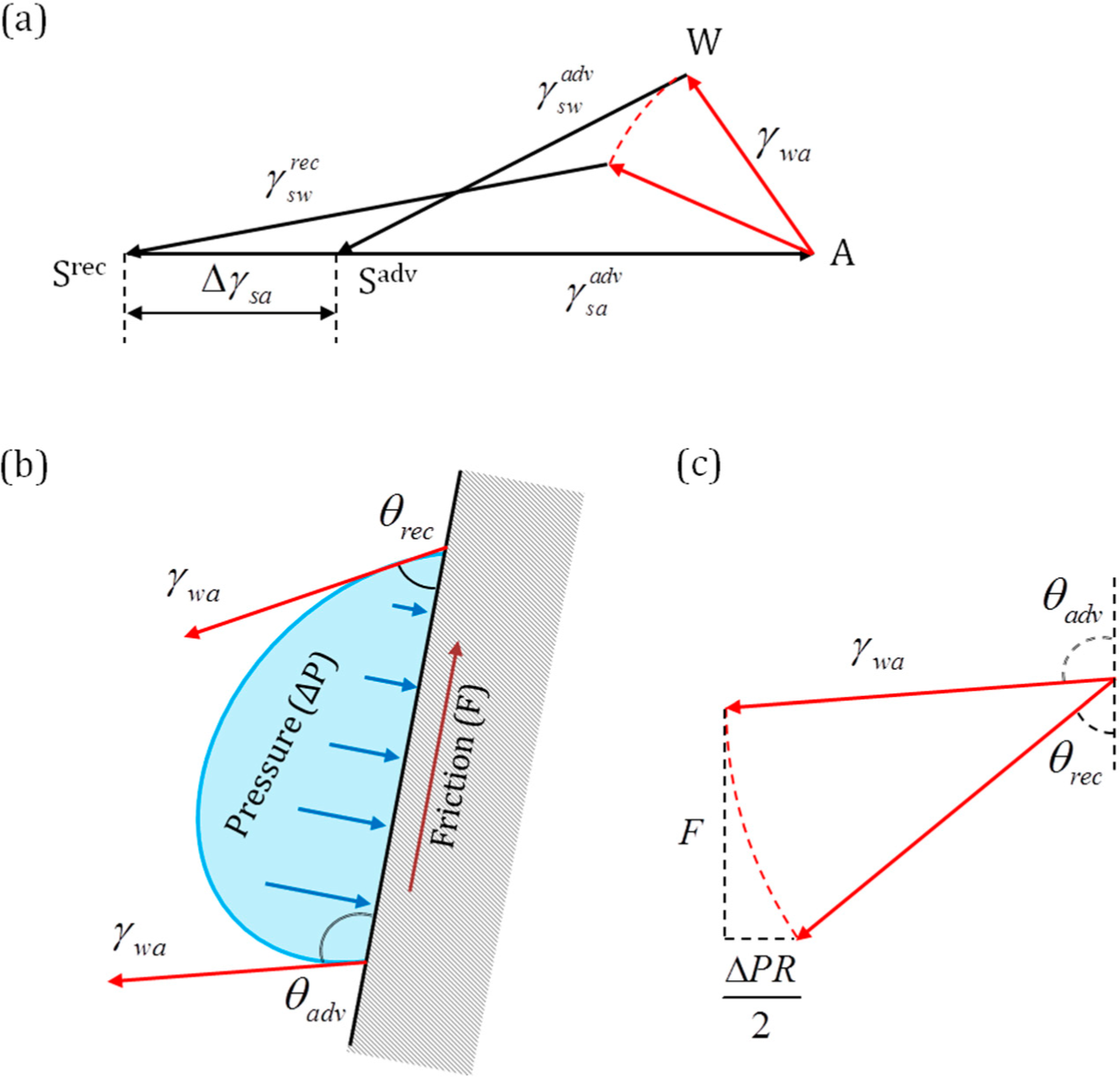
Figure 3. Other interesting geometric interpretations using the same notation. (a) Contact angle hysteresis represented using Neumann’s triangle as a rotation of the vector. A range of contact angles are possible under the constraint that remains constant. (b) The forces involved in contact angle hysteresis. For a droplet on a tilted surface, the pressure inside acting normal to the surface is the sum of Laplace, as well as hydrostatic pressures. (c) The components of the surface tension vectors normal to the surface balance the pressure force, while the components of the surface tension vectors along the surface balance the friction force.

Michael Nosonovsky and Rahul Ramachandran “Geometric Interpretation of Surface Tension Equilibrium in Superhydrophobic Systems,” Entropy 2015, 17(7), 4684-4700; doi:10.3390/e17074684