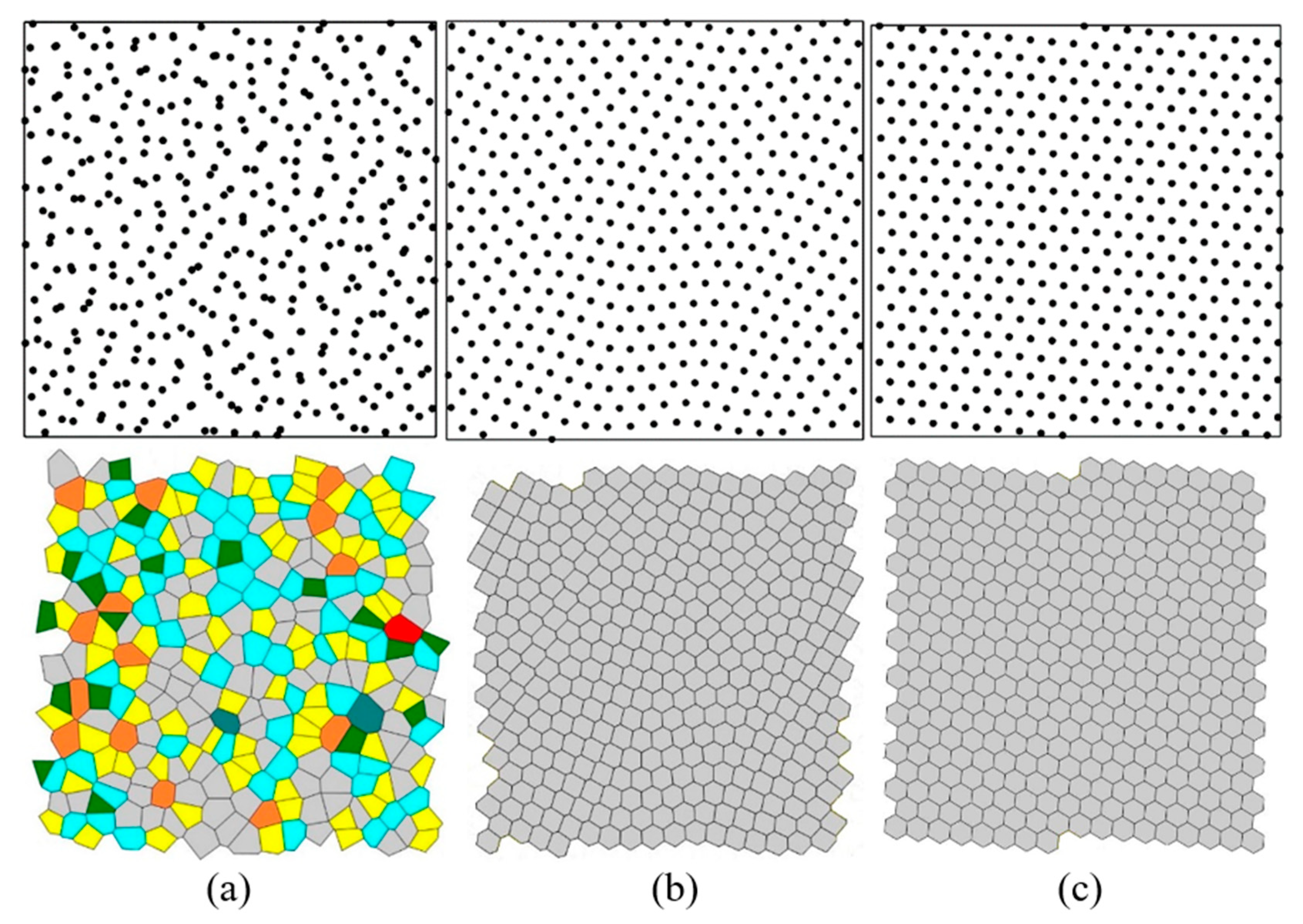
Long-range order, much like action at a distance, remains a bit mysterious. It represents an intermediate regime between perfect periodicity and complete randomness. Voronoi entropy provides a quantitative measure of order in two-dimensional point sets, ranging from S=0 for perfectly ordered configurations to 𝑆=1.690±0.001 for random point distributions, and correlates with established measures of long-range order.
Density oscillations in matter may be related to the definition of clusters as an intermediate structural level between discrete molecules and continuum descriptions. Such considerations have been discussed in contexts ranging from aperiodic crystals and quasicrystals to proposed boundaries between macroscopic (gravitational) and microscopic (quantum) regimes, sometimes associated with the Planck mass (∼10^−8 kg). While defining a scale boundary based on convergence arguments remains speculative, it poses a challenging and potentially fruitful problem.