The Voronoi Entropy of a random tessellation is S = 1.690 ± 0.001 (and not S = 1.71 as it was previously thought). Please read about it in our new paper:
The Voronoi Entropy is often used by physicists, chemists and materials scientists as a geometric measure to characterize the degree of randomness of random set of points or self-organization in such set. It changes from S=0 for a perfectly ordered pattern of points to S=1.69 for a perfectly random pattern.
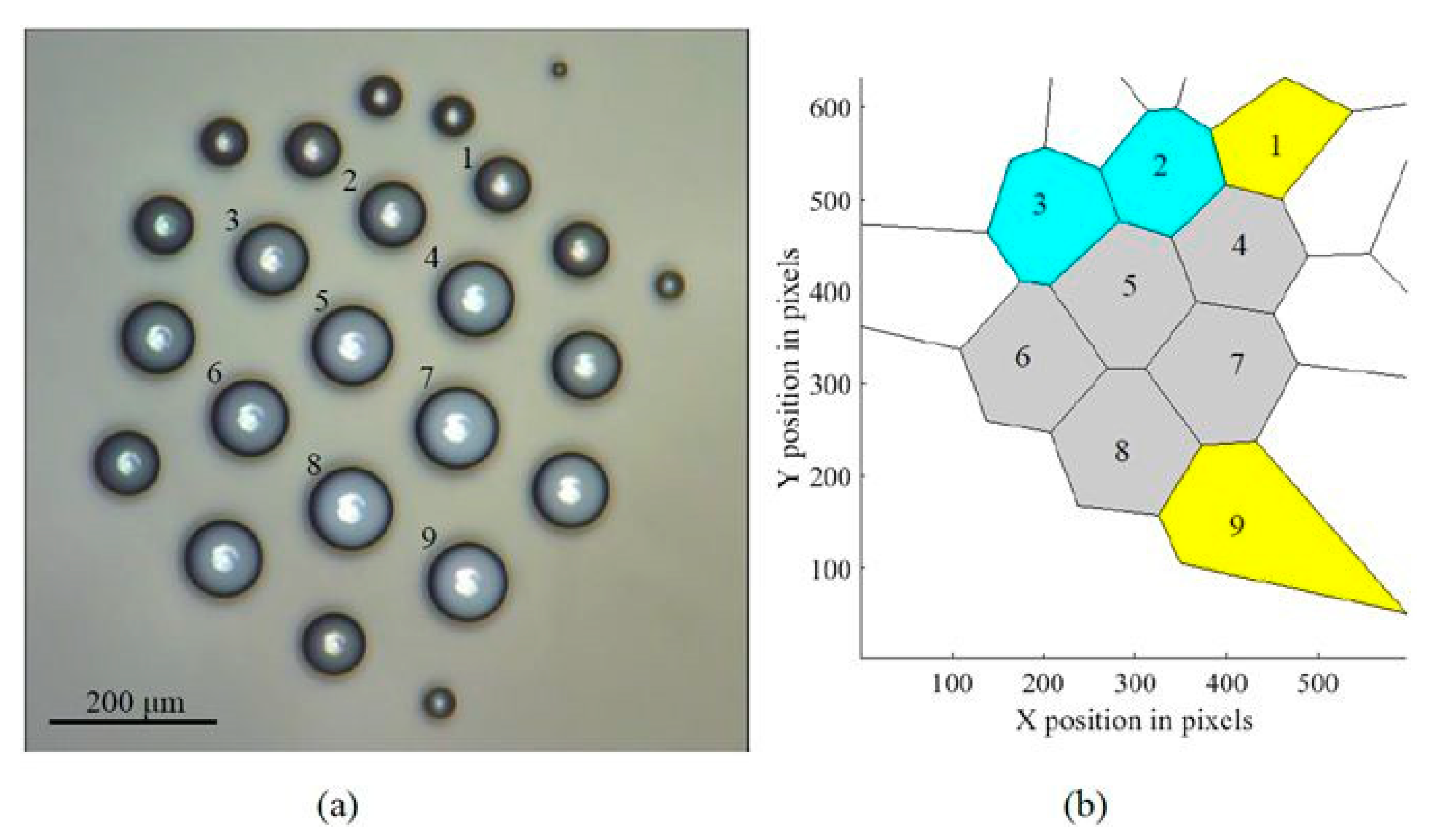
Figure: Self-organization of a droplet cluster is demonstrated. (a) The image of the cluster and (b) the Voronoi tessellation of the cluster. The scale bar is 200 µm. Yellow (1,9), gray (4–8), and blue (3,2) polygons have five, six, and seven neighbors (edges), respectively (figure reproduced with permission from Fedorets, A.A.; Frenkel, M.; Shulzinger, E.; Dombrovsky, L.A.; Bormashenko, E.; Nosonovsky, M. Self-assembled levitating clusters of water droplets: pattern-formation and stability. Sci. Rep. 2017, 7, 1888).
For more detailed discussion of the Voronoi Entropy and its history please see also our old paper Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.E.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy 2018, 20, 956. https://doi.org/10.3390/e20120956