There is a classical theory of an “entropic” elastic force in an ideal polymer chain, whose shape is modeled as a random walk. The elastic force as a function of the distance between the ends of the chain is calculated using the probability (or entropy) of a deformed configuration. For a random walk, the average total distance of travel is proportional to the square root of the number of steps, R~N1/2.
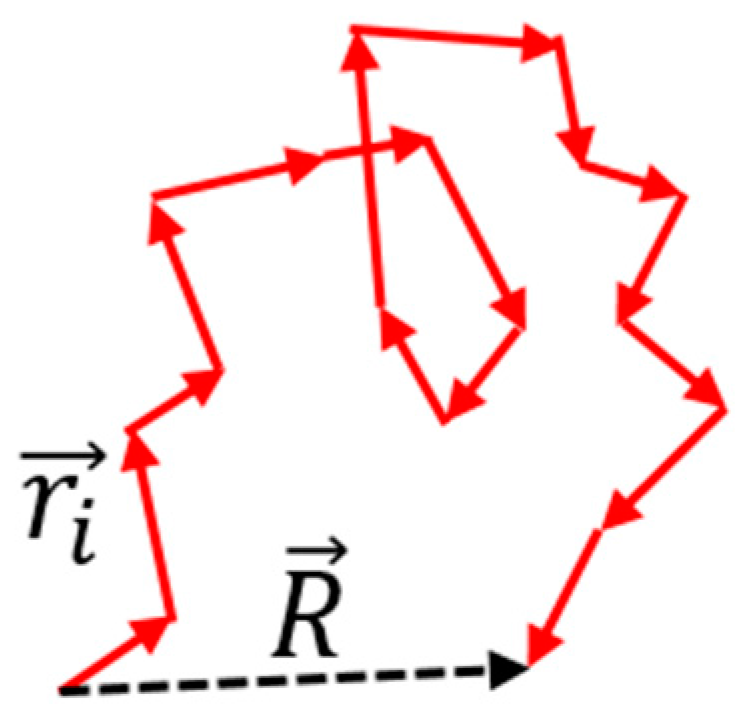
Figure 1. Random walk along an ideal polymer chain. The chain attains the most probable configuration. For a random walk, the distance is proportional to the square root of the number of steps, R~N^0.5.
In more complex non-ideal polymeric molecules (using the excluded volume approach), the end-to-end displacement and the radius of gyration are scaled as R~N3/5. More accurate estimates with the renormalization group predict the power exponent of 0.588. On the other hand, for the folded polymer chain forming a sphere, the radius of gyration is proportional to the power 1/3 of the volume, R~N1/3. Despite that, experimental data indicate that folded proteins tend to show the power exponent of 0.4 rather than 0.333. Any deviation of the power exponent from what is predicted from the scaling arguments can be interpreted as scaling of a fractal object with a fractal dimension. Thus while simple systems, such as an ideal chain or spherically folded molecules have behavior predicted from non-fractal scaling arguments, the systems with a complex structure (such as folded proteins with hydrophobic interactions between amino-acids) can demonstrate fractal behavior.
Somewhat similarly, hydrophobic liquid droplets in water would form spheres (with a 2D surface), whereas snow crystals, according to the literature, may have a fractal shape with the fractal dimension of about 1.85.
According to many researchers, protein folding is governed by the hydrophobic forces and it is controlled by self-organized criticality (SOC), which is a universal feature of hydrophobic interactions present during both wetting of hydrophobic surfaces and protein folding. Interestingly, such top experts in genetics like E. Koonin state that the folding of proteins is the main driving force of the evolution on the gene level, which also demonstrates power law and fractal quantitative behavior (however we do not want to go in depth into that area). The formation of ice (snow) crystals also demonstrates fractal characteristics typical for SOC. SOC is a special type of self-organizing behavior discussed in detail in many places on the web, so I will not discuss it here.
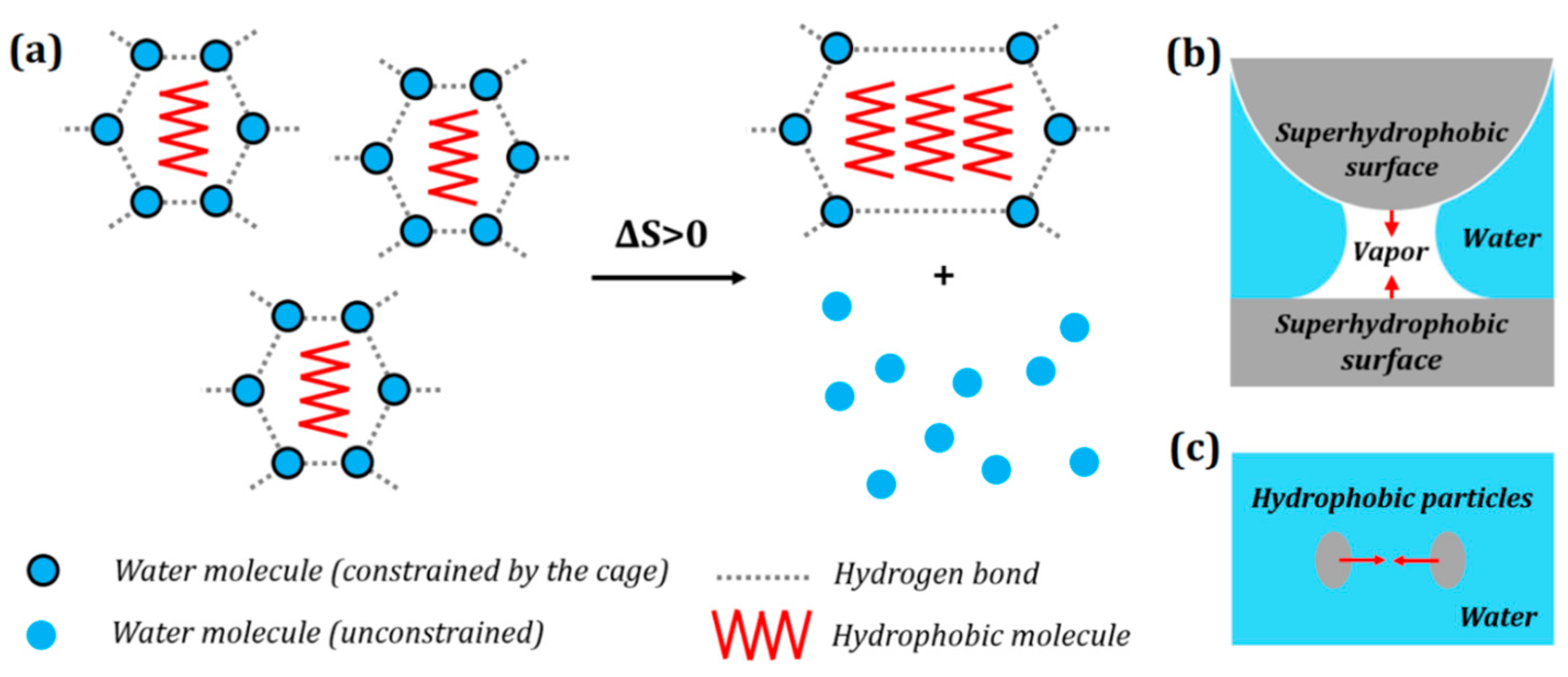
Figure 2. (a) Entropic origin of hydrophobic interaction. Aggregation of hydrophobic molecules (e.g., hydrocarbons) frees up water molecules to increase the configurational entropy of the system (attaining the most probable configuration). Hydrophobic interaction is manifested as a hydrophobic force which results in (b) clustering of hydrophobic particles in water; and (c) attraction of hydrophobic particles towards a hydrophobic surface in water.
Ice (snow) crystal formation is another process governed by interactions, which are similar to the hydrophobic forces. A hydrophobic (entropic) attraction force can emerge between a hydrophobic particle and a surface in water. However, ice crystals can form very complex structures, as opposed to a simple spherical shape formed by a hydrophobic substance in water. This is partially similar to how a protein forms a complex 3D structure as opposed to the random folding of a simple polymer chain (Figure 3). For a simple polymer chain, the most probable configuration does not depend on the shape of the polymer chain (but only on the distance between its ends). However, much more complex protein folding depends on the interaction between amino acids, and thus on the 3D shape of the molecule. Similarly, in the case of the hydrophobic attraction of two particles, the shape formed by the hydrophobic phase does not matter, since only its surface area is minimized. However, a more complex interaction of a vapor molecule with solid / ice favors certain directions or shapes (Figure 3b), and this is why snowflakes are so diverse in their shape, as opposed to spherical liquid droplets.
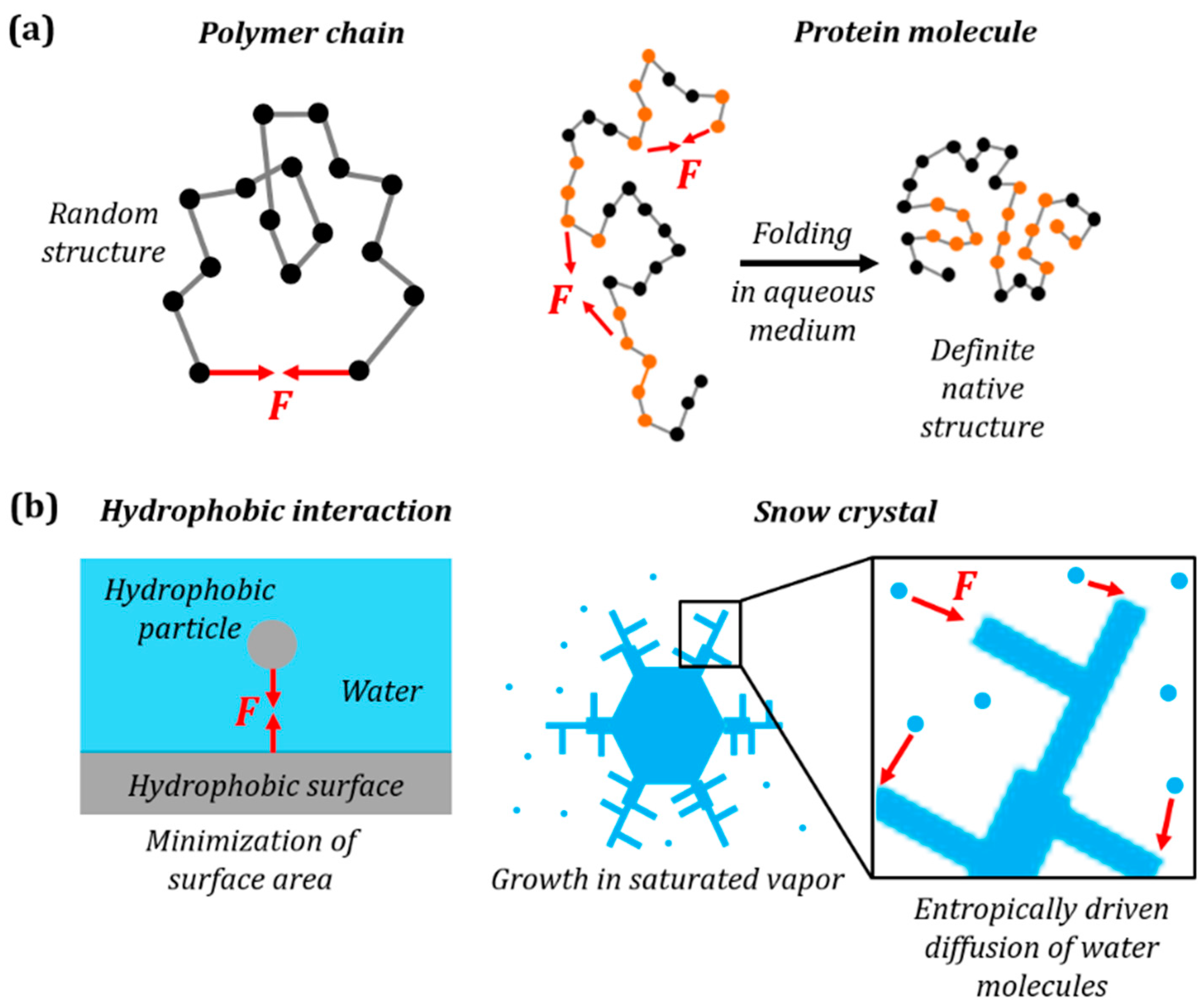
Ideal polymer chain vs. Molecules with complex structure (e.g., proteins)
Hydrophobic force in liquids vs. Interactions in ice crystal
Figure 3. (a) Folding of protein molecule from a linear primary structure to 3D tertiary (native) structure is similar to the elastic force in a polymer chain. For a polymer chain the force can be attractive or repulsive depending on the end-to-end distance. For a protein molecule the attractive hydrophobic force causes the hydrophobic side chains to retract to the interior of the cluster; (b) parallelism with snow crystal growth as opposed to the hydrophobic interaction of a particle and a surface. The red vectors denote the entropic force F in each case.
This conceptual parallelism between the ideal polymer entropic elasticity and SOC-driven folding of complex molecules on the one hand vs. hydrophobic attraction forces in liquid and complex snow crystals on the other hand is discussed in our paper
R. Ramachandran, M. Kozhukhova, K. Sobolev and M. Nosonovsky Anti-Icing Superhydrophobic Surfaces: Controlling Entropic Molecular Interactions to Design Novel Icephobic Concrete Entropy 2016, 18(4), 132; doi:10.3390/e18040132
The paper also deals with practical applications of the concept: the superhydrophobic and icephobic concrete.