| 04/30 |
- Start reading Section 4.4 (The Uniformization Theorem for Simply-connected Surfaces) for discussion next Tuesday.
- Start working on the final exam. Due 05/14.
|
| 04/25 |
- Finish reading Section 4.3 (A Classification of Riemann Surfaces) in Farkas and Kra for discussion in class on Tuesday. You may omit the Digression on page 172, and ignore the corollaries at the end of the section. There are a lot of technical details in the proof of Theorem IV.3.11; try first to pull out the big ideas of the proof, and then fill in as many of the details as you can afterwards. Send me a question on the reading by Monday evening. Due 04/29.
|
| 04/23 |
- Continue reading Section 4.3 (A Classification of Riemann Surfaces) in Farkas and Kra for discussion in class on Thursday. Try to get through at least the proof of the theorem that a Riemann surface is hyperbolic if and only if it admits Green’s functions.
- Try to classify the punctured plane
 directly from the definitions: is it elliptic, parabolic, or hyperbolic? directly from the definitions: is it elliptic, parabolic, or hyperbolic?
|
| 04/16 |
- Read Section 4.2 (Subharmonic Functions and Perron’s Method) and Section 4.3 (A Classification of Riemann Surfaces) in Farkas and Kra for discussion in class next Tuesday. Send me a question on the reading by Monday evening. Due 04/22.
- Try to prove directly from the definitions that the plane
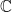 is a parabolic Riemann surface, and that the unit disk is a parabolic Riemann surface, and that the unit disk  (or, equivalently, the half plane (or, equivalently, the half plane  ) is hyperbolic. ) is hyperbolic.
|
| 04/11 |
- Read Section 4.1 (More on Harmonic Functions) in Farkas and Kra for discussion in class on Tuesday. The presentation is slightly different from that in Conway, but the material should be familiar to you. As you read, keep in mind that Farkas and Kra are working on an arbitrary Riemann surface and not on a region in
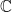 ; this occasionally requires some subtlety in the arguments. (For example, you can choose a countable dense set in any subset of a coordinate patch which is homeomorphic to a disk in ; this occasionally requires some subtlety in the arguments. (For example, you can choose a countable dense set in any subset of a coordinate patch which is homeomorphic to a disk in 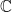 , but you cannot choose a countable dense set in the whole manifold, because you do not (yet) know that the manifold is second countable.) Do not be intimidated by the use of differential forms: they appear only in a very few formulas, and are not necessary even there. I will go over this in class, but all you really need to know is that if , but you cannot choose a countable dense set in the whole manifold, because you do not (yet) know that the manifold is second countable.) Do not be intimidated by the use of differential forms: they appear only in a very few formulas, and are not necessary even there. I will go over this in class, but all you really need to know is that if  is a function on some coordinate patch then is a function on some coordinate patch then 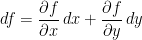 and and  . .
- (Conway) Section 10.5: 1, 3, 4
- Hand in Section 10.4: 4; Section 10.5: 4. Due 04/11.
|
| 04/09 |
- Read Section 10.5 (Green’s Function) in Conway for discussion in class on Thursday.
- Section 10.4: 3, 4.
|
| 04/04 |
- Read Section 10.4 (The Dirichlet Problem) in Conway for discussion in class on Tuesday. If you find Conway’s proof of his Theorem 4.9 rather involved (or if you object to the use of a theorem from Chapter VII that we did not cover), you could try to prove the slightly weaker result that if
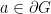 and there is a neighbourhood and there is a neighbourhood 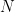 of of  such that a single-valued branch of such that a single-valued branch of  is defined in is defined in  , then there is a barrier at , then there is a barrier at  . (Hint: consider the real part of the function . (Hint: consider the real part of the function  .) This is enough to show that there is a barrier at .) This is enough to show that there is a barrier at  if if  is one endpoint of a simple curve which lies in the complement of is one endpoint of a simple curve which lies in the complement of  . .
- Section 10.3: 1, 2, 3, 4.
- Hand in Section 10.3: 3. Due 04/11.
|
| 04/02 |
- Read Section 10.3 (Subharmonic and Superharmonic Functions) in Conway for discussion in class on Thursday.
- Section 10.2: 1, 2, 3, 4, 5.
|
| 03/28 |
- Read Section 10.2 (Harmonic Functions on a Disk) in Conway for discussion in class on Tuesday.
- Section 10.1: 1, 2, 4, 5, 6 (and state and prove an analogue of this result in higher dimensions), 9, 11.
- Hand in Section 10.1: 6 (including the higher-dimensional analogue), 11. Due 04/04.
|
| 03/26 |
- Read Section 10.1 (Basic Properties of Harmonic Functions) in Conway for discussion in class on Thursday.
|
| 03/14 |
- Have a good break!
|
| 03/07 |
- Review today’s discussion, and the handout on covering transformations. Your goal this time is to understand the proof that we can classify the Riemann surfaces covered by any given simply-connected surface
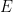 by classifying the properly-discontinuous actions by groups of conformal homeomorphisms of by classifying the properly-discontinuous actions by groups of conformal homeomorphisms of 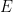 . .
|
| 03/05 |
- Review today’s discussion, and the handout on covering spaces. Your goal is to understand the proof that every analytic surface (aka Riemann surface) has a universal covering space, which can be given the structure of an analytic surface in such a way that the covering map is analytic. (Conway’s Exercise IX.7.3 is an important step to this conclusion.) Moreover, any two such covering spaces are conformally equivalent.
|
| 02/28 |
- Read Section 9.7 (Covering Spaces) for discussion in class on Tuesday.
- Your midterm exam consists of Exercises 1, 3, 4, 5, and 7 from Section 9.6. It is due on the Thursday before Spring break. Due 03/14.
|
| 02/26 |
- Finish Reading Section 9.6 (Analytic Manifolds) for discussion in class on Thursday. (You may also wish to review Section 9.5 to make sure there are no lingering questions.)
- Section 9.4: 3, 4; Section 9.5: 1, 2, 3.
|
| 02/21 |
- Read Section 9.5 (The Sheaf of Germs of Analytic Functions on an Open Set), and as much of Section 9.6 (Analytic Manifolds) as you can, for discussion in class on Tuesday. I would like us to finish reading Section 9.6 for next Thursday if possible; if you get as far as Theorem 6.9 (page 237) this time, that should enable you to make the connection between the two sections. Send me a question on the reading by Monday evening. Due 02/26.
- Section 9.3: 3, 4.
- Hand in Section 9.2: 3, 6. Due 02/28.
|
| 02/19 |
- Read Section 9.4 (Topological Spaces and Neighborhood Systems) for discussion in class on Thursday.
- Section 9.2: 1, 2, 3, 6, 7; Section 9.3: 1, 2.
|
| 02/14 |
- Read Section 9.2 (Analytic Continuation along a Path) and Section 9.3 (The Monodromy Theorem) for discussion in class on Tuesday. Send me a question on the reading by Monday evening. Due 02/18.
- Section 9.1: 1, 3.
|
| 02/07 |
- Read Section 9.1 (The Schwartz Reflection Principle) for discussion in class on Tuesday. Send me a question on the reading by Monday evening. Due 02/11.
- Section 7.4: 1, 2, 4, 5, 6, 7, 9.
- Hand in Section 7.7: 6; Section 7.4: 9. Due 02/14.
|
| 02/05 |
- Read Section 7.4 (The Riemann Mapping Theorem) for discussion in class on Thursday.
- Section 7.7: 4, 5, 6, 8.
|
| 01/24 |
- Read Section 7.7 (The Gamma Function) for discussion in class on Tuesday. Send me a question on the reading by Monday evening. Due 01/28.
- Section 4.6: 2, 3, 4, 6, 9.
|
| 01/22 |
- Read Section 4.6 (The Homotopic Version of Cauchy’s Theorem and Simple Connectivity) for discussion in class on Thursday.
|