| 05/07 |
- Work on your final exam. Due 05/13.
- Have a safe and happy summer!
|
| 05/06 |
- (Optional) Watch this video on Divergence and Curl: The Language of Maxwell’s Equations, Fluid Flow, and More from 3Blue1Brown.
- Section 19.4: 1, 2, 5, 17, 20, 21, 22, 24, 28, 29, 34, 36.
|
| 05/05 |
- Read Section 19.4 (The Divergence Theorem) and the Section 19.4 Divergence Theorem summary.
- Watch this video on 3D Divergence Theorem Intuition from Khan Academy. Note that Khan actually starts the video talking about the 2-dimensional Divergence Theorem (which, as you know from the summary, is really just Green’s Theorem in disguise).
- Section 19.3: 1, 3, 4, 9, 11, 12, 14, 16, 17, 20, 21, 30, 31.
|
| 05/04 |
- Read Section 19.3 (The Divergence of a Vector Field) and the Section 19.3 Divergence of a Vector Field summary.
- Watch these two videos on Divergence Intuition, Part 1 and Divergence Intuition, Part 2 from Khan Academy. (You might also find the other videos in this series to be useful. In particular, Khan has a nice way of thinking about the algebraic formula for the divergence, although in my opinion the best motivation is the one in our textbook, starting from the geometric definition.) Note that Khan’s discussion concerns only 2-dimensional vector fields, but everything he says can be generalized to the 3-dimensional case.
- Section 19.1: 1, 4, 5, 6, 7, 9, 11, 13, 15, 16, 20, 27, 29, 35, 43, 49, 68, 69, 72, 73, 74, 76, 79, 82.
|
| 04/30 |
- Read Section 19.1 (The Idea of a Flux Integral) and the Section 19.1 The Idea of a Flux Integral summary.
- Watch this video on Conceptual Understanding of Flux from Khan Academy.
- Hand in Project 2. Due today, 04/30.
- Hand in Section 18.2: 36; Section 18.3: 36; Section 18.4: 34. Due 05/05.
|
| 04/29 |
- Finish reading Section 18.4 (Path-Dependent Vector Fields and Green’s Theorem), and re-read the summary, if necessary. Concentrate on understanding the statement of Green’s Theorem: we can discuss the proof in class if you find it challenging.
- Section 18.4: 3, 5, 9, 10, 13, 16, 17, 19, 20, 24, 25, 26, 27, 29, 31, 34, 38, 39, 40, 41, 45, 47, 48.
- Complete your second project.
|
| 04/28 |
- Start reading Section 18.4 (Path-Dependent Vector Fields and Green’s Theorem) and the Section 18.4 Path-Dependent Vector Fields and Green’s Theorem summary. This is a long section, so don’t feel you have to get all the way through it. Do try to get through the first two sections: how to tell whether a vector field is path-independent using line integrals, and using the curl. Send me a question on this reading by tomorrow evening. Due 05/29.
- Watch this video on Green’s Theorem (Example 1) from Khan Academy. (Optional: watch Example 2, also; it is the next video in the series.)
- Section 18.3: 1, 3, 4, 5, 7, 8, 13, 15, 17, 19, 25, 27, 30, 35, 36, 44, 45, 46, 49, 50, 55, 62.
|
| 04/27 |
- Read Section 18.3 (Gradient Fields and Path-Independent Fields) and the Section 18.3 Gradient Fields and Path-Independent Fields summary.
- Watch this video on Closed Curve Line Integrals of Conservative Fields from Khan Academy. (Two comments. First, notice that Khan does not define a vector field to be conservative if it integrates to 0 around any closed curve, as we did. Instead, he defines a conservative field as one which is the gradient of a scalar function. We know these properties are equivalent, so it really doesn’t matter which one we take as the definition. Second, Khan uses a special notation
 for the line integral around a closed curve.) for the line integral around a closed curve.)
- Section 18.2: 2, 5, 7, 12, 17, 20, 23, 34, 35, 36, 41, 42, 47, 49, 53, 55.
- Continue working on Project 2. Remember that the project is due this Thursday. Let me know as soon as possible if you think you will have trouble finishing in time. Due 04/30.
|
| 04/23 |
- Read Section 18.2 (Computing Line Integrals over Parametrized Curves) and the Section 18.2 Computing Line Integrals over Parametrized Curves summary.
- Watch this video on Using a Line Integral to Find Work from Khan Academy.
- Section 18.1: 3, 4, 6, 13, 17, 18, 20, 23, 24, 27, 28, 36, 44, 48, 49, 58, 59, 62, 64, 65, 67.
- Hand in your second project progress report. Due Today.
- Hand in Section 17.2: 50; Section 17.3: 36; Section 18.1: 24, 48. Due 04/28.
|
| 04/22 |
- Read Section 18.1 (The Idea of a Line Integral) and the Section 18.1 Idea of a Line Integral summary.
- Watch this video on Line Integrals and Vector Fields from Khan Academy. (You will watch the next video in the sequence tomorrow; the later ones also cover good material, but we will study those topics later.)
- Section 17.4: 3, 5, 8, 11, 16, 18, 19, 21, 22, 24, 25, 28, 29, 21, 33, 34, 35.
|
| 04/21 |
- Read Section 17.4 (The Flow of a Vector Field) and the Section 17.4 Flow of a Vector Field summary. Send me a question on this reading by tomorow evening. Due 04/22.
- Watch this video on Fluid Flow and Vector Fields from Khan Academy.
- Section 17.3: 4, 5, 7, 10, 11, 15, 16, 17, 20, 21, 27, 30, 33, 34, 36, 39, 40.
|
| 04/20 |
- Read Section 17.3 (Vector Fields) and the Section 17.3 Vector Fields summary.
- Watch this video on Vector Fields, Introduction from Khan Academy. Note that Khan writes his vectors vertically&emdash;as columns&emdash;rather than horizontally. This is actually quite a common convention, so it is useful for you to see an example of it. (The 3 videos following this one in the series are also useful; you will be assigned one as an official reading tomorrow.)
- Section 16.5: 1, 2, 4, 6, 8, 10, 12, 13, 16, 21, 22, 23, 35, 44, 48, 51, 55, 73, 75.
- Work on your project. Remember that your second progress report is due this Thursday, 04/23.
|
| 04/16 |
- Read Section 16.5 (Integrals in Cylindrical and Spherical Co-ordinates) and the 16.5 Integrals in Cylindrical and Spherical Co-ordinates summary.
- Watch this video on Converting Triple Integrals to Cylindrical Coordinates. As with yesterday’s video, stop the video as soon as you see the iterated integral that is going to be converted, and ask yourself: what is the 3-dimensional region that is being integrated over; \textit{i.e.}\ try to write the given iterated integral as a triple integral. (This time, the lecturer does not show the region later in the video!). Also, at the end of the video, ask yourself whether the final answer could have been obtained more easily.
- (Optional) Watch this video on Triple Integral in Spherical Coordinates to Find Volume. (There is an error in the conversion equations on the board at the start of the video. What is it?)
- Section 16.4: 3, 9, 13, 15, 17, 19, 21, 22, 25, 27, 29, 30, 35, 37, 38, 41.
- Hand in Section 16.2: 50; Section 16.3: 36, 60; Section 16.4: 29. Due 04/21.
|
| 04/15 |
- Read Section 16.4 (Double Integrals in Polar Coordinates) and the 16.4 Double Integrals in Polar Co-ordinates summary.
- Watch this video on Converting Iterated Integrals to Polar Coordinates. Stop the video as soon as you see the iterated integral that is going to be converted, and ask yourself: what is the 2-dimensional region that is being integrated over; i.e. try to write the given iterated integral as a double integral. (You will see the region later in the video, but you should try to work it out for yourself first.)
- Section 16.3: 5, 6, 10, 11, 16, 17, 18, 21, 22, 23, 27, 29, 31, 33, 36, 39, 42, 43, 46, 49, 51, 52, 53, 57, 60, 61, 62, 70, 71, 74, 75, 77, 78, 81, 82.
|
| 04/14 |
- Read Section 16.3 (Triple Integrals) and the 16.3 Triple Integrals summary. Send me a question on this reading by tomorrow evaning. Due 04/15.
- Watch this video on Triple Integrals, Changing the Order of Integration, Part 1 of 3. Although the title of the video refers to changing the order of integration, what the lecturer actually does is write a triple integral as an iterated integral in two different ways. (If you find this useful, you can watch the remaining 2~parts, in which apparently he sets up yet more iterated integrals for the same triple integral!)
- Section 16.2: 2, 3, 7, 11, 13, 14, 17, 19, 20, 23, 27, 29, 32, 35, 36, 39, 41, 45, 47, 49, 50, 52, 55, 59, 68, 70, 72, 73, 74, 75.
|
| 04/13 |
- Read Section 16.2 (Iterated Integrals) and the 16.2 Iterated Integrals summary.
- Watch this video on Regions of Integration from MIT Opencourseware. The lecturer evaluates two double integrals, one fairly straightforward, and one more involved, and evaluates each of them in two ways. (Note, however, that he does not write either of them as being with respect to $dA$ initially.)
- Section 16.1: 1, 3, 5, 7, 9, 14, 15, 17, 18, 19, 22, 23, 25, 27, 28.
|
| 04/09 |
- Read Section 16.1 (The Definite Integral of a Function of Two Variables) and the 16.1 Definite Integral of a Function of Two Variables summaryfor discussion in class on Monday.
- Watch this video from Professor Leonard on INTRODUCTION to Double Integrals. Be careful with the notation: Professor Leonard uses
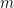 for the number of subintervals in the for the number of subintervals in the  direction, and direction, and  for the number in the for the number in the  direction, which is the reverse of what I did in my summary. This makes no difference to the final result, of course. (Professor Leonard’s other videos are also good, but long. This one, however, is `only’ 38 minutes long.) direction, which is the reverse of what I did in my summary. This makes no difference to the final result, of course. (Professor Leonard’s other videos are also good, but long. This one, however, is `only’ 38 minutes long.)
- Section 15.3: 20, 22, 23, 24, 25, 29, 33, 34, 36, 39, 42, 49, 50, 56, 59, 61.
- Hand in your Project 2 Progress Report. You may just e-mail this to me, one copy per group please. Due today, 04/09.
- Hand in Section 15.2: 14; Section 15.3: 17. Due 04/14.
|
| 04/08 |
- Finish reading Section 15.3 (Constrained Optimization: Lagrange Multipliers).
- Watch the third, fourth and fifth videos in the Khan Academy series on constrained optimization. (The videos you should watch this time are “Finishing the Intro: Lagrange Multiplier Example”, “Lagrange Multiplier Example, Part 1” and “Lagrange Multiplier Example, Part 2”.) The remaining videos in the series are also very good. Feel free to watch them if you have found the earlier ones to be useful, but they are definitely optional.)
- Section 15.3: 1, 3, 9, 17, 18, 19.
|
| 04/07 |
- Read the first parts of Section 15.3 (Constrained Optimization: Lagrange Multipliers) and all of the 15.3 Constrained Optimization summary. In the textbook, try to get through the subsection “Lagrange Multipliers in General”; you can stop when you get to “Optimization with Inequality Constraints”. Send me a question on this reading by tomorrow evening. Due 04/08.
- Watch the first two videos in this series of Khan Academy videos on constrained optimizztion. (The two videos you should watch are “Constrained Optimization: Introduction” and “Lagrange Multipliers: Using Tangency to Solve Constrained Optimization”. They give you a somewhat different way of thinking about Lagrange multipliers than the approach I describe in my summary, but perhaps closer to the approach taken in the textbook.)
- Section 15.2: 1, 3, 5, 7, 11, 13, 14, 17, 21, 25, 31, 32, 33, 34, 37, 43, 46.
|
| 04/06 |
- Read Section 15.2 (Optimization) and the 15.2 Optimization summary.
- Section 15.1: 1, 3, 5, 7, 9, 17, 21, 25, 26, 27, 29, 31, 33, 35, 36, 39, 41, 43, 53, 54.
|
| 04/02 |
- Read Section 15.1 (Critical Points: Local Extrema and Saddle Points) and the 15.1 Critical Points summary.
- Watch this video from Khan Academy on Multivariable Maxima and Minima. As with the other Khan Academy link we have seenm this actually leads you to a series of videos. You should watch the second one (Saddle Points) also. The remaining videos in the series are optional, unleass you want to be learn a lot more about the Second Derivative Test for functions of two variables.
- Section 14.8: 1, 3, 5, 14, 17.
- Hand in Section 14.6: 32; Section 14.7: 28, 29, 31; Section 14.8: 17. Due 04/07.
(Note For the remainder of the semester, you will hand in assigned problems by taking a picture of your solutions with your cell phone—or scanning them in some other way—and uploading the file to the assignment dropbox in Canvas.)
|
| 04/01 |
- Read Section 14.8 (Differentiability) and the Section 14.8 Differentiability summary.
- Watch all or part of this video on Differentiability of Two Variable Functions. The complete video is good, but long (about 1~hour). If you watch just from 9:20 through 16:30, however, you will see a summary on a slide of the 1-variable case, and a very nice visual demonstration of what goes wrong in the 2-variable case. (If you want to watch the entire video, you may have to rewind it to the start: on my browser it startsa few minutes in.)
- Section 14.7: 3, 6, 12, 16, 21, 24, 25, 28, 29, 31, 37, 40, 41, 45, 47, 49, 55, 61, 62, 63.
|
| 03/31 |
- Read Section 14.7 (Second-Order Partial Derivatives) and the Section 14.7 Second-Order Partial Derivatives summary.
- Watch this video on Second-Order Partial Derivatives.
- Any of Section 14.6: 1, 3, 9, 13, 15, 16, 18, 19, 21, 23, 25, 32, 34, 37, 45, 46, 47, that you did not complete before the break.
|
| 03/30 |
- Welcome back!
- You were asked to read Section 14.6 (The Chain Rule) more than once before our extended break. As a refresher, read Section 14.6 The Chain Rule summary.
- Watch this video on The Multivariable Chain Rule from Khan Academy.
This link will actually take you to a sequence of 5 videos. You only need to watch the first of these, but of course you may watch any of them that you please. In my opinion, the first 3 are all very good, the fourth (on directional deriva- tives) is rather confusing, and the last one is good but chal- lenging. (In this last video, the presenter is giving a rigorous proof of the Chain Rule and, as I suggest in my summary, there is no way around the fact that that proof is just long and complicated.)
|
| 03/12 |
- Have a good break!
|
| 03/11 |
- Review for the midterm exam.
|
| 03/10 |
- Prepare questions for the midterm review session in class tomorrow.
- Review for the midterm exam.
|
| 03/09 |
- Re-read Section 14.6 (The Chain Rule) for discussion in class tomorrow. (Try to get to the end of the section this time.)
- Section 14.6: 1, 3, 9, 13, 15, 16, 18, 19, 21, 23, 25, 32, 34, 45, 46, 47.
- Review for the midterm exam, which will be given in class this Thursday, 03/12.
|
| 03/05 |
- Read Section 14.6 (The Chain Rule) for discussion in class on Monday. (The main idea is in the section “The Chain Rule for
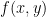 , ,  , , 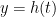 “, so you can concentrate most of your effort on that section, but try to get to the end if you can.) “, so you can concentrate most of your effort on that section, but try to get to the end if you can.)
- Section 14.5: 3, 7, 11, 17, 21, 24, 25, 29, 31, 33, 35, 37, 43, 45, 48, 50, 51, 52, 61, 62, 64, 70, 71, 75, 77, 79.
- Hand in Section 14.4: 52, 81; Section 14.5: 48. Due 03/10.
|
| 03/04 |
- Read Section 14.5 (Gradients and Directional Derivatives in Space) for discussion in class tomorrow.
- Section 14.4: 3, 11, 19, 27, 33, 35, 43, 49, 52, 55, 59, 65, 73, 77, 82, 83, 89, 90, 94, 95, 99, 100.
|
| 03/03 |
- Read Section 14.4 (Gradients and Directional Derivatives in the Plane) for discussion in class on Wednesday.
- Section 14.1: 3, 5, 15, 17, 21, 23, 25, 29, 34, 41, 43, 47.
- Section 14.2: 5, 7, 15, 23, 35, 39, 45, 47, 48, 50, 51.
|
| 03/02 |
- Read Sections 14.1 (The Partial Derivative) and 14.2 (Computing Partial Derivatives Algebraically) for discussion in class tomorrow.
- Section 12.6: 1, 3, 13, 17, 19, 23, 24, 25, 29.
|
| 02/27 |
- Read Section 12.6 (Limits and Continuity) for discussion in class on Monday.
- Section 12.5: 1, 2, 3, 7, 16, 18, 19, 21, 26, 29, 32, 34, 37, 45, 47, 48, 52, 53.
- Hand in Section 12.2: 19(a)(c)(f) (explain your reasons for your choices); Section 12.4: 17; Section 12.5: 52, 53. Due 03/03.
|
| 02/26 |
- Read Section 12.5 (Functions of Three variables) for discussion in class on Thursday.
- Section 12.3: 1, 16, 21, 25, 31.
- Section 12.4: 9, 15, 17, 21, 22, 23.
|
| 02/25 |
- Read Sections 12.3 (Contour Diagrams) and 12.4 (Linear Functions) for discussion in class on Wednesday.
- Section 12.1: 3, 5, 7, 10, 18-20, 21, 23, 25, 26, 27, 33, 38, 42, 45, 46, 52, 53.
- Section 12.2: 1, 3, 19(a)(c)(f) (explain your reasons for your choices), 22, 24, 25, 30, 33, 37, 39.
|
| 02/24 |
- Read Section 12.1 (Functions of Two Variables) and 12.2 (Graphs and Surfaces) for discussion in class tomorrow.
- Section 10.4: 3, 6, 9, 11, 17, 18, 21, 23, 29-33.
|
| 02/20 |
Complete your projects, and hand them in on Monday. Due 02/24.
Update Projects are now due one week from this Monday. Due 03/02.
|
| 02/19 |
- Read Section 10.4 (The Error in Taylor Polynomial Approximations) for discussion in class on Thursday.
- Section 10.3: 3, 7, 11, 13, 23, 25, 26, 27, 29, 35, 38, 40, 41, 4345, 47, 49, 51, 53.
|
| 02/18 |
- Continue working on your projects.
|
| 02/17 |
- Read Section 10.3 (Finding and Using Taylor Series) for discussion in class on Wednesday.
- Section 10.2: 1, 6, 7, 9, 13, 15, 17, 19, 21 (and try to prove that this is the Taylor series for
 ), 23, 24, 25, 27, 29, 32, 33, 34, 35, 37, 39, 43, 45, 47, 51, 52, 54. ), 23, 24, 25, 27, 29, 32, 33, 34, 35, 37, 39, 43, 45, 47, 51, 52, 54.
- Homework originally due on Tuesday is now due Wednesday. Due 02/19.
|
| 02/13 |
- Read Section 10.2 (Taylor Series) for discussion on Monday.
- Section 10.1: 1, 3, 5, 13, 17, 18, 19, 21, 23, 24, 29, 30, 31, 32, 33, 37, 40, 42, 43, 46, 49, 50, 51, 53.
- Hand in Section 9.5: 30, 48; Section 10.1: 18, 19. Due 02/18.
|
| 02/12 |
- Read Section 10.1 (Taylor Polynomials) for discussion on Thursday.
- Section 9.5: 1, 3, 5, 9, 11, 13, 15, 17, 24, 25, 29, 30, 32, 35, 39, 43, 45, 46, 47, 48.
|
| 02/11 |
- Re-read Section 9.5 (Power Series and Interval of Convergence) for discussion on Wednesday.
- Catch up with any remaining homework from Section 9.4.
|
| 02/10 |
- No formal homework today, but take the time to make sure you undderstand the ideas in Sections 9.3 and 9.4.
|
| 02/06 |
- Work on your projects, and prepare your progress report. Due 02/10.
- Hand in Section 9.3: 46; Section 9.4: 66, 85. Due 02/11.
|
| 02/05 |
- Read Section 9.5 (Power Series and Interval of Convergence) for discussion on Monday.
- Catch up with any remaining homework from Section 9.4.
|
| 02/04 |
- Read as much as you can of Section 9.4 (Tests for Convergence). This is a long section, with a lot of ideas, but try to understand at least the Comparison, Limit Comparison, and Ratio Tests. Keep in mind the general principle that a series (at least a series of positive terms) should converge if the terms go to zero “fast enough”. How does the Comparison Test reflect this principle, for example?
- Section 9.4: 1, 2, 3, 5, 9, 11, 13, 15, 16, 19, 21, 23, 25, 27, 39, 41, 45, 47, 55, 63, 65, 66, 73, 75, 79, 85, 87, 88, 93, 96, 97, 103, 104, 106, 107, 115, 116.
|
| 02/03 |
- Re-read Section 9.3 (Convergence of Series) in light of today’s discussion. (You can still omit the section on comparison of series and integrals.) Also, study the notes on convergence and divergence of the
 -series on the “Additional Notes and Files” page; these notes will complete the last problem of the exercise set we worked on today, and we will clarify any issues with them—especially the last computation—on Monday. -series on the “Additional Notes and Files” page; these notes will complete the last problem of the exercise set we worked on today, and we will clarify any issues with them—especially the last computation—on Monday.
- Section 9.3: 1, 13, 17, 19, 25, 27, 31, 35, 38, 46, 47(b) (this one is a challenge!), 53, 55, 56, 57, 58, 61, 62, 63, 65. Avoid using the Integral Test or any of these, since we have not studied it yet.
- Work on your project. Send me an e-mail to let me knokw who is in your project roup. (One e-mail per group is sufficient.) The project is Due 02/24. Your progress report is due one week from today, 02/10.
|
| 01/30 |
- Read Section 9.3 (Convergence of Series) for discussion on Monday. You can give a light reading to the material on comparison of series and integrals if you are not familiar with improper integrals. (We did not cover that topic last semester, but we will do so soon, and will discuss the Integral Test then.)
- Section 9.2: 1, 3, 5, 7, 9, 13, 21, 25, 27, 31, 33, 34, 37, 41, 43, 46, 47, 50-54.
- Hand in Section 9.1: 40, 68; Section 9.2: 46. Due 02/04.
|
| 01/29 |
- Read Section 9.2 (Geometric Series) for discussion in class tomorrow.
- Section 9.1: 5, 11, 13, 17, 23, 25, 29, 31, 37, 40, 41, 45, 49, 54, 55, 57, 59, 63, 67, 68, 69.
|
| 01/28 |
- Read Section 9.1 (Sequences) for discussion in class tomorrow.
- Review the questions on the “Introduction to Sequences and Series” worksheet. In particular, think about the final exercise, and be ready to present your solution in class tomorrow.
|
| 01/27 |
- Review Sections 17.1 (Parametrized Curves) and 17.2 (Motion, Velocity and Acceleration) for discussion in class tomorrow.
- Decide on your groups for Project 1, which will be handed out this week.
|
| 01/23 |
- Work on the question posed at the end of class today: given non-zero vectors
 and and  in 3-dimensional space, find a non-zero vector in 3-dimensional space, find a non-zero vector 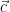 which is orthogonal to both of them. Thinking of the geometric interpretation of the dot product, this means we want which is orthogonal to both of them. Thinking of the geometric interpretation of the dot product, this means we want 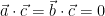 ; in terms of components, we have to solve the system of equations ; in terms of components, we have to solve the system of equations  and and 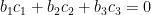 for the unknowns for the unknowns 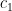 , ,  , and , and  in terms of the in terms of the  ‘s and ‘s and 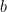 ‘s. ‘s.
- Read Section 13.4 (The Cross Product) for discussion in class on Monday.
- Section 13.3: 1, 9, 11, 13, 15, 19, 23, 25, 27, 29, 32, 33, 37, 39, 40, 43, 47, 53, 55, 56, 57, 59, 63 (you don’t have to do all of the properties, but verify some of them), 68. (Optional: 69. This will require you to do 66 and 67 first.)
- Section 13.4: 5, 9, 11, 12, 13, 15, 19, 21, 25, 26, 29, 35, 41, 42, 43, 45, 47, 48, 49, 54, 55, 56, 58, 60, 62, 65, 67.
- Hand in Section 13.3: 55; Section 13.4: 25, 26, 42. Due 01/28.
|
| 01/22 |
- Read Section 13.3 (The Dot Product) for discussion in class tomorrow.
- Section 13.1: 1, 5, 9, 15, 23, 25, 31, 33, 38, 39, 41, 44, 45, 47, 51, 57, 58, 59, 60.
- Section 13.2: 3, 5, 9, 13, 15, 19, 23, 25, 29, 30, 32, 33, 37, 38, 39, 41, 43 through 48.
|
| 01/21 |
- Read Section 13.2 (Vectors in General) for discussion tomorrow (Wednesday). You might want to review Section 13.1 (Displacement Vectors) also, but we did see much of that material last semester.
|