| 05/08
|
- Read the next section in Rudin (Stokes Theorem) for discussion in class on Thursday. Note that the proof of the theorem essentially proceeds by unpacking definitions until we arrive at a simple special case, where the integrals can be explicitly evaluated. (We will also discuss the application of these ideas to vector analysis on Thursday, so feel free to read ahead if you wish.)
- Work on your final exam.
|
| 05/03
|
- Read the next section in Rudin (Simplexes and Chains), through the end of subsection 10.30, for discussion in class on Tuesday. (You do not have to read about positively oriented boundaries at this point.) Send me a questions on the reading by Monday evening. Due 05/07.
- Complete Chapter 10: Exercises 15, 18, 20, 21.
- Your final exam consists of 5 exercises from Rudin: C7-16, C7-18, C8-13, C9-27, C10-21. (Notation: C7-16 refers to Exercise 16 from Chapter 7.) All but one of these have been assigned at the appropriate point in the semester, so you may have solutions to them already written. If so, please take the time to look over your solution(s) in light of your later experience in the class, and re-write them as you see fit. The exam is due on the scheduled exam day for the class, Saturday, May 12, at 12:00 noon.
|
| 05/01
|
- Finish reading the section on Differential Forms for discussion on Thursday. Pay particular attention to the definition of the pullback form ωT on 10.21, and to the displayed equation in Theorem 10.25. (Why do I call ωT “pullback”? Does that concept help to make sense of the formula in 10.25? Drawing a diagram of the situation will also probably help.)
|
| 04/26
|
- Read as much as you can of the next section from Chapter 10 (Differential Forms) for discussion on Tuesday. Hopefully, you can manage through at least to the end of 10.17; i.e. everything before the sub-section on “Differentiation”. You do not need to send me a question on the reading but, as always, feel free to do so if anything is not clear.
- Complete Chapter 10: Exercises 9, 10, 12, 13.
- Hand in Chapter 10, Exercises 12 and 13. Due 05/03.
|
| 04/24
|
- Read the next two sections from Chapter 10 (Partitions of Unity, and Change of Variables) for discussion on Thursday. (Our next reading will be the very long section on Differential Forms, so if the assigned reading goes quickly, and you have extra time to spend on this course, feel free to read ahead.)
- Complete Chapter 10: Exercises 2, 4, 6.
|
| 04/19
|
- Read the first two sections from Chapter 10 (Integration, and Primitive Mappings) for discussion on Tuesday. You do not need to send me a question on the reading but, as always, feel free to do so if anything is not clear.
- Complete Chapter 9: Exercises 29, 30, 31.
- Hand in Chapter 9, Exercise 30. Due 04/26.
|
| 04/17
|
- Read the last section from Chapter 9 (Differentiation of Integrals) for discussion on Thursday.
- Complete Chapter 9: Exercises 21, 23, 26, 27, 28.
|
| 04/10
|
- Read the sections on Determinants, and on Derivatives of Higher Order, for discussion next Tuesday. (We will also continue our discussion of the Implicit Function Theorem that day, if desired; we will omit the Rank Theorem.) Send me a question on the reading by Monday evening. Due 04/16.
- During Thursday’s class, work together on Exercises 17, 18, 19, 20 from Chapter 10 of Rudin. (The Jacobian of a mapping is mentioned in Exercise 17; the definition is on page 234.) Complete for homework any of these exercises that were not completed during the class period.
|
| 04/05
|
- Read the next two sections in Chapter 9 (The Inverse Function Theorem, and The Implicit Function Theorem), for discussion in class on Tuesday. Send me a question on the reading by Monday evening. Due 04/09.
- Hand in Chapter 8, Exercise 17 (including the extension to functions of bounded variation); Chapter 9, Exercise 14. Due 04/12.
|
| 04/03
|
- Complete Chapter 9: Exercises 6, 7, 8, 9, 10, 14. (Optional: any remaining exercise, 1-15.)
- Read the next section in Chapter 9 (The Contraction Principle) for discussion in class on Thursday.
|
| 03/27
|
- Complete Chapter 8: Exercises 12, 13, 15, 16, 17. (You may also be interested in Exercise 14 and the reference included therein.)
- Read the first section in Chapter 9 (Linear Transformations) for discussion in class on Thursday. This is quite a long section, so don’t worry if you don’t manage to finish it, but hopefully much of it will be familiar to you.
|
| 03/08
|
- Complete the midterm exam. Due 03/13.
- Continue reading the section on Fourier Series in Rudin. As you read, try to make connections to today’s discussion of orthonormal sets in inner product spaces.
|
| 02/27
|
- Begin work on the midterm exam. Due 03/13.
- Begin reading the section on Fourier Series in Rudin, for discussion in class next Tuesday.
|
| 02/22 |
- Read Michael Wichura’s notes on interchanging summations (handed out in class, and on the “Additional Notes” page; if you use the online version, read only pages 10-1 through 10-5).
- Read or re-read the next two sections in Rudin (The Exponential and Logarithm Functions, and The Trigonometric Functions) for discussion in class on Tuesday.
- Complete Chapter 8: Exercises 7, 8, 9, 10.
|
| 02/20 |
- Read the next section in Rudin (The Exponential and Logarithm Functions) for discussion in class on Thursday.
- Complete Chapter 8: Exercises 2, 3, 4, 6.
|
| 02/15 |
- Read (as much as you can of) the first section in Chapter 8 of Rudin (Power Series). Send me a question on the reading by Monday evening. Due 02/19.
- Complete Chapter 8: Exercise 1. (We haven’t shown how to differentiate the exponential function yet, but you know how to do it!)
- Hand in Nothing. Zilch. Nada.
|
| 02/13 |
- Re-read the section in Rudin on the Stone-Weierstrass Theorem in light of today’s discussion, and send me any remaining questions before Thursday’s class.
|
| 02/08 |
- Send me any remaining questions on the Stone-Weierstrass Theorem by Monday evening. Due 02/12.
- Complete Chapter 5: Exercises 28, 29; Chapter 7: Exercise 26.
- Hand in Chapter 7: Exercises 24, 25. Due 02/15.
|
| 02/06 |
- Read the final section of Chapter 7 in Rudin (The Stone-Weierstrass Theorem). You do not need to send me a question on this reading, but feel free to do so if anything is not clear. (Do not be concerned if you find this a challenging reading. It is one of the most abstract topics we will discuss this smester, and we will take as much time as necessary to understand it thoroughly.)
- Complete Chapter 7: Exercises 24 and 25.
|
| 02/01 |
- Read the next sections of Chapter 7 in Rudin (Equicontinuous Families of Functions). Send me a question on the reading by Monday evening. Due 02/05.
- Complete Chapter 7: Exercises 14, 15, 16, 18, 19.
- Hand in Chapter 7: Exercises 13, 19. Due 02/08.
|
| 01/30 |
- Read the next section of Chapter 7 in Rudin (Uniform Convergence and Differentiation). You do not need to send me a question on this reading, but feel free to do so if anything is not clear.
- Complete Chapter 7: Exercise 13.
|
| 01/25 |
- Read the next two sections of Chapter 7 in Rudin (Uniform Convergence and Continuity, and Uniform Convergence and Integration). Send me a question on the reading by Monday evening. Due01/29.
- Complete Chapter 7: Exercises 4 through 10.
- Hand in Chapter 7: Exercises 2 (
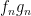 only), 3, 6. Due 02/01. only), 3, 6. Due 02/01.
|
| 01/23 |
- Take a quick look through the first 6 chapters of Rudin to see if there are any topics you would like us to discuss or review. Bring those topics to class on Thursday.
- Read the first two sections of Chapter 7 in Rudin (Discussion of Main Problem, and Uniform Convergence). Send me a question on the reading by Wednesday evening. Due 01/24.
- Think about Exercises 1, 2, 3 from Chapter 7 of Rudin. (You do not need to solve them completely, but use them to inform you reading.)
|